Many of life’s decisions boil down to the following dilemma: would you rather settle for a guaranteed reward or take a risk by exploring what other rewards are available? Mathematically, we can characterize this dilemma as a tradeoff between some fixed, known reward and some random sample from a probability distribution, such as the ubiquitous normal distribution. In the simplest version of this dilemma, where the probability distribution is known and your risk preferences are assumed to be neutral, the correct choice is obvious: take the guaranteed reward when it’s greater than the mean of the distribution you’d sample from, and take your chance with the random reward otherwise.
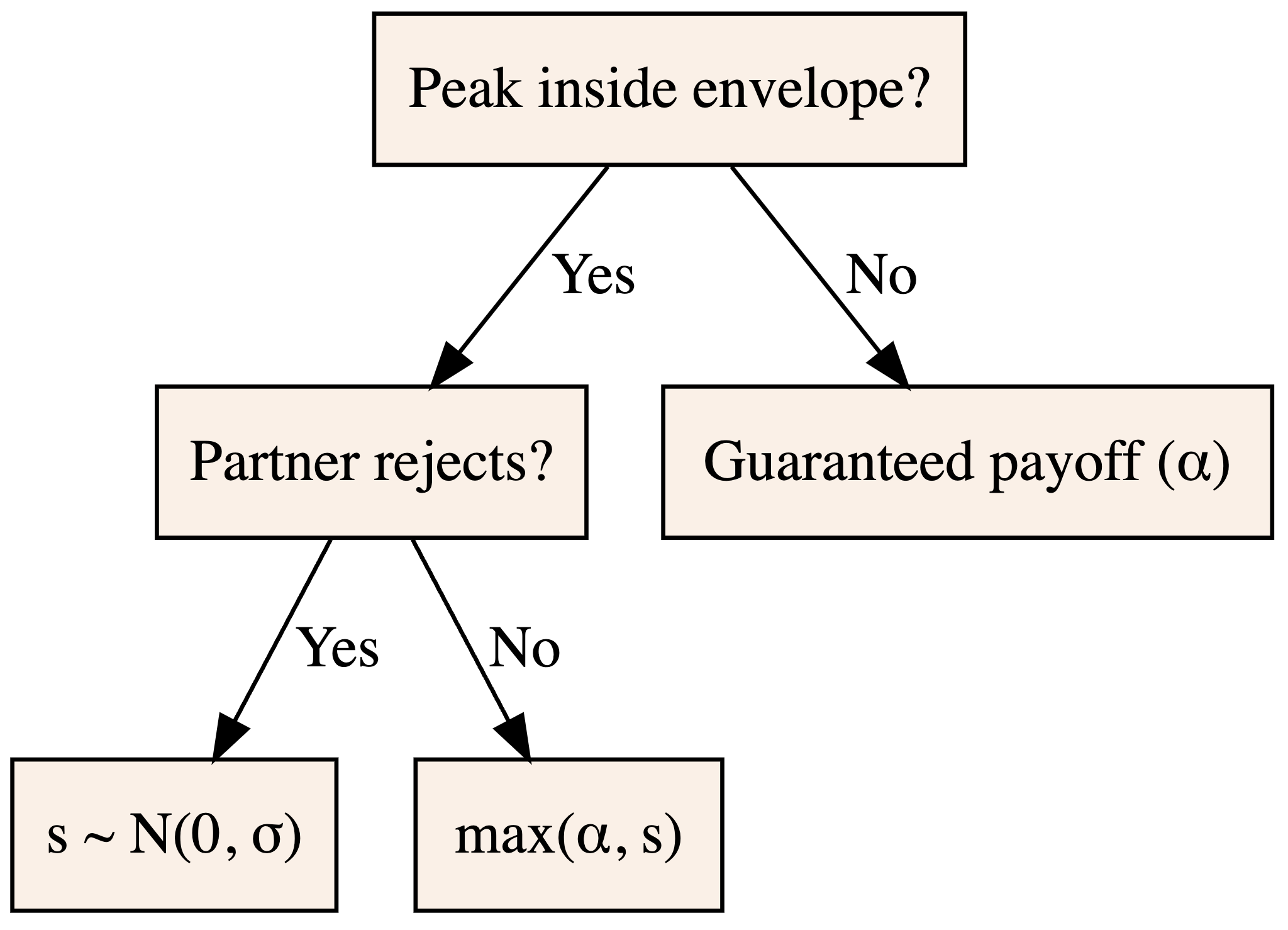
But, sometimes, you don’t need to choose. With a guarantee of some positive reward, you can costlessly explore whether there’s a better option. If there is, you can take that option; if there’s not, you can fall back on the guaranteed reward. In other words, you end up with the maximum of a sampled reward and your guaranteed reward, which is at least as good as either option on its own.
Notably, exploration is still valuable even if the mean of the distribution you’re sampling from is well below the guaranteed reward. Since you’re not forced to take the option you sample if it’s less than your guaranteed reward, you only care about the possibility of sampling a value above this guaranteed reward. For the normal distributions we’ll be considering here, this possibility is dictated by both the mean and the variance of the distribution. A distribution with a low mean but high variance offers many possibilities of high rewards.
Concretely, let’s assume (without loss of generality) that you sample rewards from a normal distribution centered on 0 with some variance \(\sigma^2\). The guaranteed reward is some value \(\alpha > 0\), i.e., larger than the mean of the outside distribution. How does your expected reward from taking the max of the sampled value and \(\alpha\) depend on the distribution’s standard deviation (square root of variance), \(\sigma\)? Intuitively, if \(\sigma\) is close to 0, you know that the draw you get will be close to the mean of the distribution (0), which is less than the guaranteed reward. In contrast, if \(\sigma\) is large, there’s a much better chance of sampling a large number that exceeds \(\alpha\). Formally, your expected reward is just the mean of a left-censored normal distribution (i.e., a normal distribution where all the values below \(\alpha\) are replaced with \(\alpha\)). The plot below shows how the mean of this distribution depends in a close-to-linear way on the standard deviation of the latent normal distribution we’re sampling from (with \(\alpha\) set to 1).
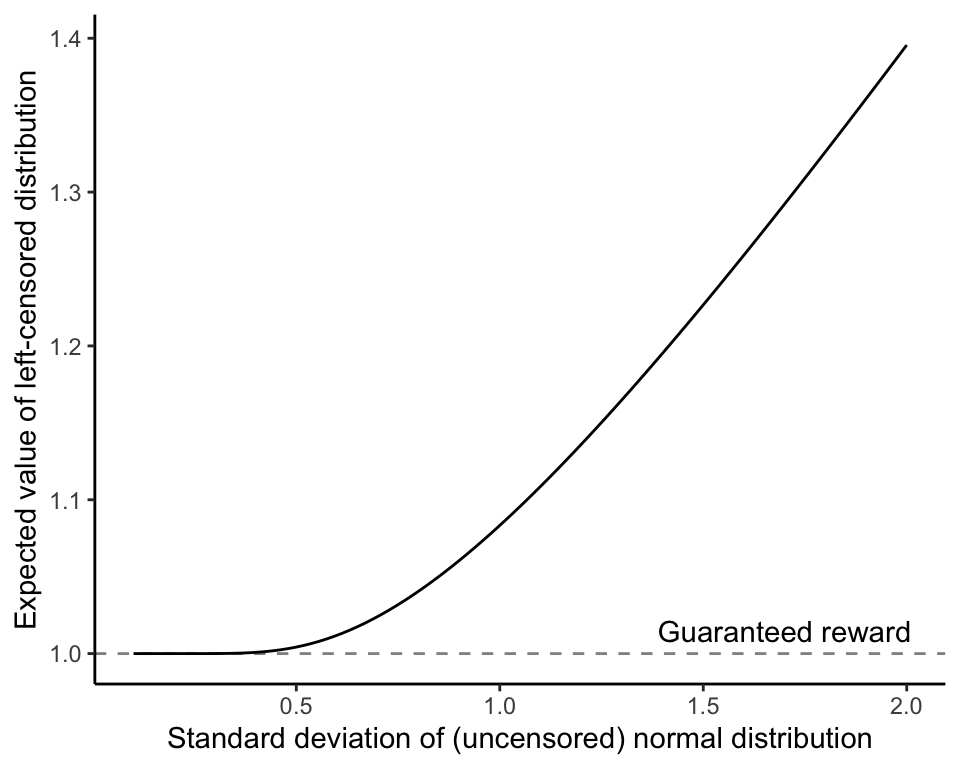
The life lesson is clear: even when there’s a reasonably good option to fall back on, it pays off to be able to look around (i.e., sample from a distribution of other options) before committing to this safe option. You’ll end up with a reward at least as good as your guaranteed reward. And it’s particularly advantageous to peak at outside options when there’s a lot of uncertainty about what you might find, since this will increase the odds that you’ll find a better-than-safe reward.
But what happens when this ‘safe’ option isn’t fully guaranteed? Specifically, what happens when your temptation to explore outside options is precisely what undermines your chances of securing the \(\alpha\) payoff — because your decision to explore is observable and potentially costly to the social partner you count on for this safe reward? This is the question posed by one my favorite papers, from Moshe Hoffman, Erez Yoeli, and Martin Nowak.
Modeling the social costs of exploration
This post was inspired by the “envelope game” — the toy game-theoretic model from Hoffman et al.’s paper that purports to explain social phenomena as diverse as “authentic altruism, why people cooperate intuitively, one-shot cooperation, why friends do not keep track of favors, why we admire principled people, Kant’s second formulation of the Categorical Imperative, taboos, and love.” For a full account of how the model relates to these social behaviors, I encourage you to take a few minutes to read the paper, which is rich in detail. But, briefly, the envelope game is meant to describe any kind of asymmetric relationship in which you are tempted to gather information (inside a metaphorical envelope) that could risk harming another party with whom you have an ongoing relationship. The other party would therefore prefer that you don’t gather this information, and they can withold their future cooperative behavior if you seek it out. Hoffman et al.’s key insight is that there are some conditions under which it is payoff maximizing for you to forego gathering this useful information and “cooperate without looking.”
The game most obviously describes romantic contexts, in which you might be tempted1 to shop around for other possible partners while in a relationship, but your current partner would suffer from your abandoning them.2 Therefore, your current partner will demand that you don’t ‘look’ at other options, and, if your partner exceeds some threshold of acceptability, you will want to signal to them that you’re not searching for other partners — perhaps by demonstrating that you’re madly in love with them.3 Similar dynamics apply in friendships and some other types of relationships. For example, if an acquaintance asks for help moving, you may be tempted to find out how many boxes there are or how long the move will take so that you can make up an excuse to defect if the task seems too onerous. But asking such questions is often considered taboo, as your acquaintance doesn’t want to invest in a friendship with somebody who calculates the costs of favors. Therefore, insofar as this is a relationship you’d like to invest in, you want to signal that you’re a principled person who agrees to help without asking these kinds of questions.
In this post, I will be focusing on some mathematical details of the game, which could have implications for these kinds of real-world situations. As I summarize the game, I’ll mostly ignore game theory concepts. Although the authors would surely argue that these concepts are critical to understanding the model, I somewhat disagree. For our purposes, we can focus on the payoff of a focal player, who I’ll continue to refer to as “you,” and subsume the other player (who I call your “partner,” with gender-neutral pronouns) into your ‘environment.’4 In doing so, I implicitly assume your partner is acting in their self interest without giving them explicit payoffs.
The original envelope game
You are presented with a metaphorical envelope that contains a randomly sampled “temptation” reward. There are only two possible payoffs in the envelope — a lower, more common reward and a higher, rarer reward. You choose whether to look at the temptation inside the envelope, and your partner chooses whether to pay a cost to deliver a known reward to you, \(\alpha\), based on whether you opened the envelope.5
Your partner is always willing to deliver \(\alpha\) to you if you don’t open the envelope — i.e., if you forego sampling a reward. But they may not be willing to deliver this benefit to you if you look inside the envelope (because, e.g., they risk being abandoned for another partner). It’s assumed that your partner will deterministically refuse to deliver \(\alpha\) to you if you open the envelope and there’s any chance that you’ll abandon them, i.e., if at least the higher reward is larger than \(\alpha\).
If \(\alpha\) is larger than both possible temptations, your partner doesn’t care if you look inside the envelope, and you have no reason to look. If \(\alpha\) is smaller than both possible temptations, it’s always worth it for you to look, and you don’t care if your partner rejects you. The interesting parameter region is therefore the one in which \(\alpha\) is between the low and high temptation. In this region, your partner will reject you for looking, so you are faced with the dilemma of whether to (i) accept a guaranteed \(\alpha\) without peaking inside the envelope or (ii) sample from the temptation distribution in the envelope and be stuck with whatever reward you find. We’ve encountered this dilemma before: you should accept the guaranteed \(\alpha\) if and only if it’s larger than the average envelope reward. The cases where \(\alpha\) is this large are the ones where there’s “cooperation without looking” — people strategically avoiding useful information to signal commitment.
In short, the paper provides a fascinating existence proof for a certain class of social behaviors. But under what conditions should we expect these behaviors in the real world? The original model is so idealized that it’s somewhat limited in its ability to make concrete predictions. Although the additions we’ll explore here are still quite abstract, I hope they can build on the original results. We’ll particularly home in on the nature of your temptations and your partner’s sensitivity to them.
A new envelope game
First, let’s add some complexity to the temptation distribution. Real ‘temptations’ in the world are rarely dichotomous; it’s more reasonable to assume, because of the central limit theorem, that they follow an approximately bell-shaped distribution. So, as we did in the beginning of this post, we’ll assume the reward in the envelope is a sample from a normal distribution with a mean of 0 and some variance \(\sigma^2\).
This complicates your partner’s decision. Now, there is always some nonzero probability of sampling a better payoff than \(\alpha\) because a normal distribution can take on any value. But, presumably, your partner is willing to tolerate a small chance of your defecting.6 So let’s suppose that your partner can condition their behavior on the probability that your temptation payoff is greater than \(\alpha\). As this probability increases — and it becomes more likely that you will succumb to the temptation if you look inside the envelope — they become less likely to want to partner with you.
As discussed earlier, the probability that the envelope payoff, which we’ll call \(s\) (for sample), exceeds \(\alpha\) is a function of the normal distribution’s standard deviation, \(\sigma\). (It also depends on the mean, but we’ve fixed this at 0 while allowing \(\alpha\) to vary.) This probability, \(P(s > \alpha)\), is calculated from \(\Phi\), i.e., the cumulative density function of a standard normal: \(1 - \Phi(\alpha / \sigma)\). Your partner’s probability of rejecting you for looking at the temptation payoff (i.e., denying you the option of falling back on the safe payoff of \(\alpha\)) should increase with \(P(s > \alpha)\). It should approach 1 when \(P(s > \alpha)\) is large and 0 when \(P(s > \alpha)\) is small. Because we’ve assumed \(\alpha > 0\), and hence the temptation distribution has a lower mean than your partner’s guaranteed reward for you if you eschew looking inside the envelope, you should never look in the limiting cases in which your partner is guaranteed to reject you. The logic here is exactly the same as that of the original model. But now we can explore a more ambiguous set of cases in which your rejection probability is between 0 and 1.
What counts as a “large” or “small” \(P(s > \alpha)\) will depend on your partner’s tolerance for uncertainty and bargaining power. Rather than explicitly model your partner’s incentives and costs, we simply assume that they have some tolerance probability for being abandoned. Let the parameter \(\rho\) capture the exact \(P(s > \alpha)\) between 0 and 1 at which your partner is indifferent between accepting or rejecting you for looking inside the envelope. In other words, when \(P(s > \alpha) = \rho\), there’s a 50-50 chance you’ll be offered the safe payoff \(\alpha\), and a 50-50 chance you’ll be forced to accept the temptation payoff \(s\) even when \(s < \alpha\). When \(P(s > \alpha) < \rho\), your partner is more likely than not to accept you if you look; and when \(P(s > \alpha) > \rho\), your partner is more likely than not to reject you if you look. Your payoff for not looking is always \(\alpha\), regardless of \(\rho\).
Critically, let’s assume — as is common in cognitive modeling — that the rejection probability for looking doesn’t transition immediately from 0 to 100% around the \(\rho\) threshold. In most real-world contexts, people’s decisions exhibit noise, especially near an indifference point. (The noise in this case could reflect both your partner’s uncertainty about whether to punish or stay with you and their inability to perfectly detect whether you looked at outside options.) Let’s therefore model your partner’s probability of rejecting you using a logistic function centered on \(\rho\) with some sensitivity (aka inverse temperature) parameter \(\beta\), which controls how responsive this rejection probability is to small changes in \(P(s > \alpha)\):
\[ P(\text{rejection})=\frac{1}{1 + e^{-\beta(P(s > \alpha)-\rho)}}. \]
Decreasing \(\beta\) increases noise around the \(\rho\) threshold. For example, the red line below has \(\rho = 0.32\) with a high sensitivity of \(\beta = 100\), and the blue line has \(\rho = 0.38\) with a lower sensitivity of \(\beta = 10\).
We can make the same plot with \(\sigma\) on the x-axis, which I’ve log-scaled for clarity. This highlights how a low \(\beta\) can force the probability of rejection to stay well below 1 even for extremely variable envelope distributions, while at the same time increasing the probability of rejection for lower \(\sigma\) values. This will turn out to have some interesting implications.
We now have all the ingredients to explore our modified envelope game. In short, you are faced with a decision to (i) look inside the envelope for a better option, but risk getting caught and rejected or (ii) ignore the envelope and lock in a guaranteed benefit \(\alpha\) from a prospective partner. The payoffs from these two strategies will depend on (a) how much better \(\alpha\) is relative to the mean of the envelope’s distribution (fixed at 0); (b) how variable the envelope’s distribution is, \(\sigma\); and (c) your partner’s willingness to let you look inside the envelope before committing to them, which we capture with the logistic parameters \(\rho\) (indifference point) and \(\beta\) (sensitivity). Your final payoff is summarized in the diagram below.
When should you look?
Effects of your partner’s tolerance
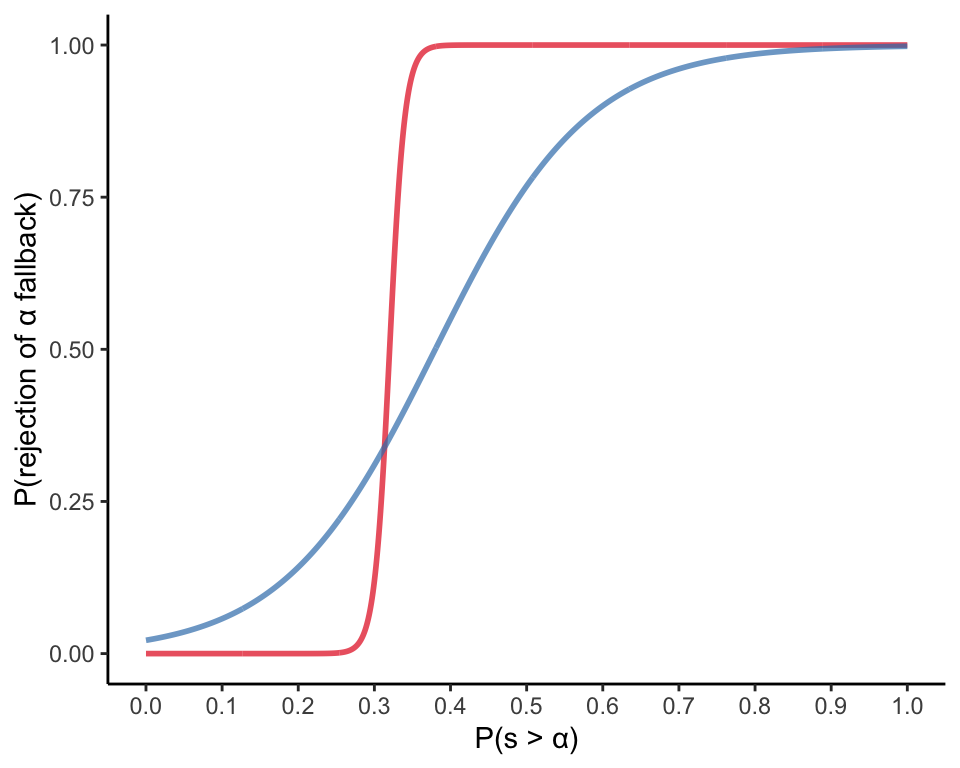
Let’s start by focusing on the tolerance parameter, \(\rho\). Intuitively, if your partner won’t tolerate even a small probability of your leaving them (low \(\rho\)), it’s better not to open the envelope — provided the \(\alpha\) payoff they can offer you is sufficiently high. As tolerance increases, there should come a point where it’s better to open the envelope, since your risk of rejection is low. As \(\rho\) approaches 1, we approach the world in which there’s no risk from looking, and your expected reward is just the expected value of the left-censored normal distribution that we discussed earlier (with \(\alpha\) as the censored value). The rate of this transition should scale with the sensitivity of the logistic function, \(\beta\). This is what we see below, where we hold fixed the standard deviation of the envelope distribution at 1 and then vary \(\rho\) for a couple combinations of \(\alpha\) (dotted horizontal lines) and \(\beta\) (colors).
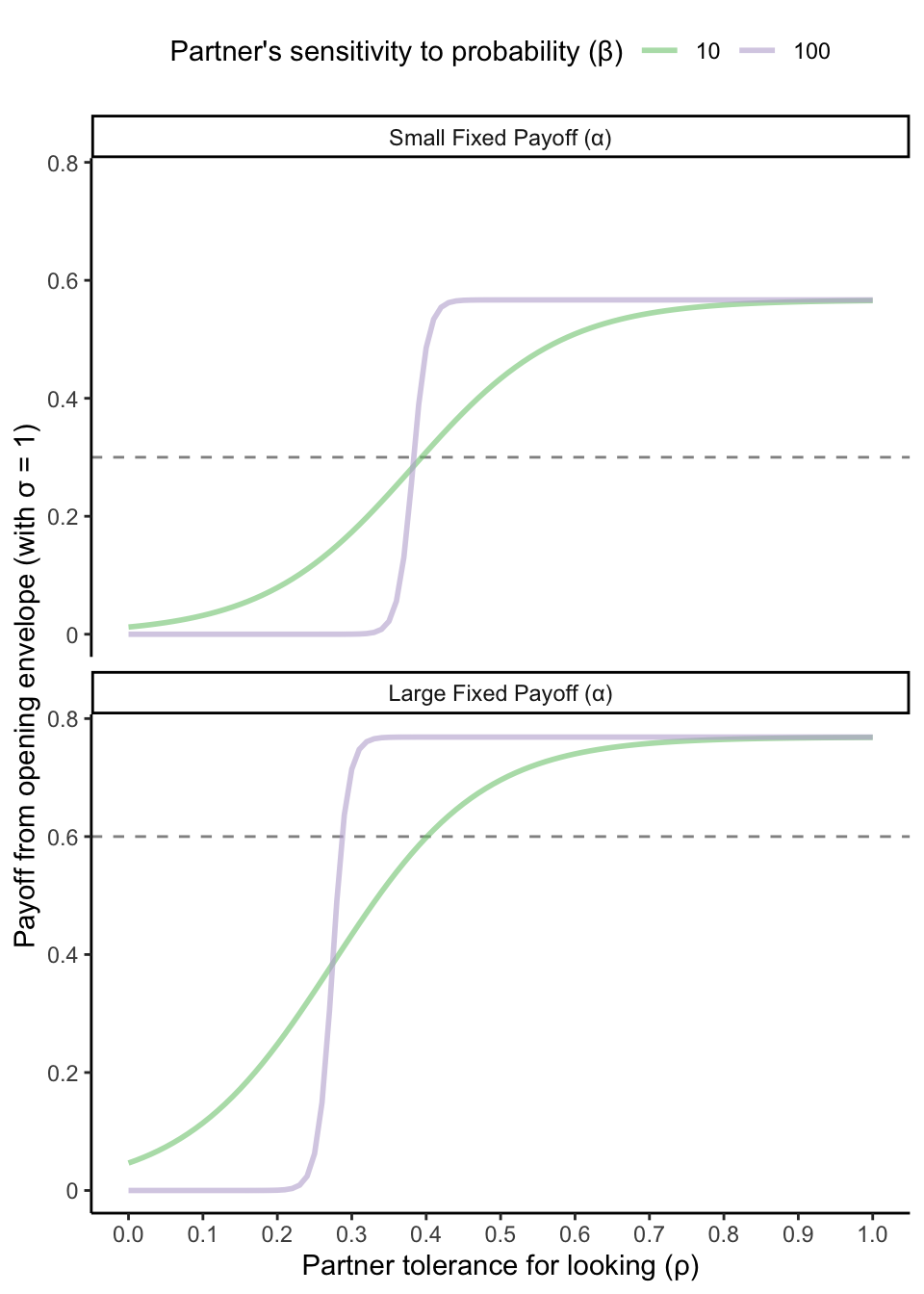
The figure above further suggests that the range of \(\rho\) that matters for the relative payoffs of the looking versus not-looking strategies is fairly small, especially when \(\beta\) is large. In other words, there may be a lot of contexts in which it’s obvious from your partner’s attitudes that you’ll be rejected for seeking outside options and vice versa. On the other hand, the smalll region of \(\rho\) that matters could be a more common one if your partner’s tolerance for looking is calibrated to the quality of your outside options, as might be the case in market-like conditions (e.g., romantic relationships).
With this in mind, let’s zoom in on the region of \(\rho\) where the payoff from looking inside the envelope is close to the payoff from foregoing this risk. How does \(\sigma\) affect these payoffs within this band of tolerances? Recall that there are two competing forces at work: (i) larger \(\sigma\) implies a higher probability of finding a better outside option in the envelope; but (ii) it also reduces the probability that you can rely on your partner’s safe payoff, \(\alpha\). If you cannot rely on \(\alpha\), the mean of the envelope distribution (0) will determine your expected payoff from looking, rather than the standard deviation, \(\sigma\).
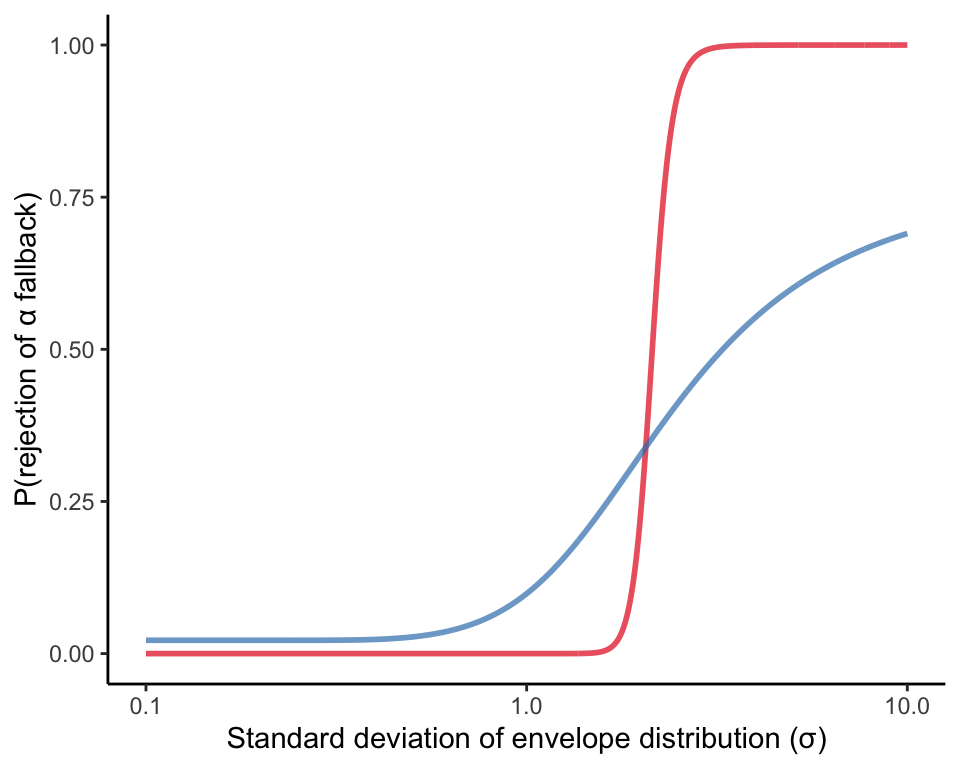
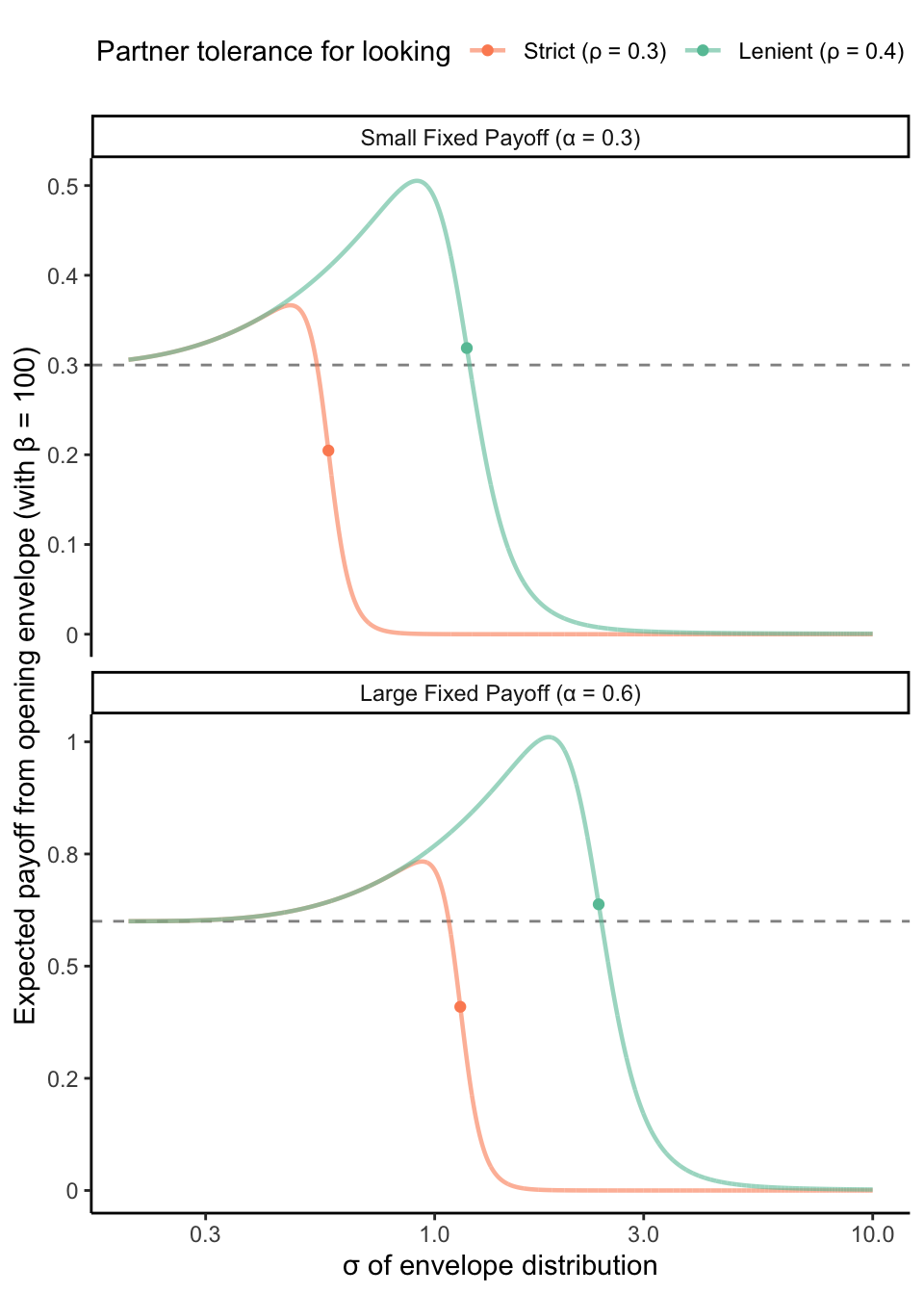
The impact of \(\sigma\) will be sharpest when there’s a sharp transition between acceptable and unacceptable looking, i.e., when \(\beta\) is high. So let’s begin by considering the regime with \(\beta = 100\), which is the closest analog to the original envelope game. When we vary \(\sigma\) in the plot below (note the log scale on the x-axis), we notice a fairly straightforward pattern. For envelope distributions with relatively low variances, looking inside is a winning strategy, relative to sticking with the guaranteed safe payoff, \(\alpha\) (indicated by the dotted line). This advantage ramps up at first, but then quickly collapses. The magnitude of the looking advantage reaches a higher peak for the more lenient (green) partner.
As expected, the collapse of the looking strategy coincides with your partner’s rapidly increasing rejection probability for your opening the envelope. Specifically, the point on each line indicates the \(\sigma\) for which your partner is indifferent between your looking and not looking — i.e., the point at which you are 50% likely to be rejected for looking. Your expected payoff from looking begins to drop before this indifferent point is reached.
Interestingly, the rejection probability at which the looking payoff falls below the not looking payoff — and you’d therefore prefer not to open the envelope — depends on your partner’s tolerance, \(\rho\). For the stricter partners (orange lines), this transition occurs before your partner’s indifference point; for the more lenient partners (green lines), it occurs after. Moreover, this basic relationship does not depend on \(\alpha\). While doubling \(\alpha\) doubles the \(\sigma\) at which the expected payoff between looking and not looking are equal, the rejection probability where this happens is only determined by \(\rho\) (and, as we’ll see later, \(\beta\)).
In the plot below, we can more clearly see this relationship between \(\rho\) and the rejection probability at which you want to switch to a not-looking strategy. When tolerance is high, you’re willing to risk an almost 4 out of 5 chance of getting rejected in order to look inside the envelope, while the opposite holds when tolerance is low.
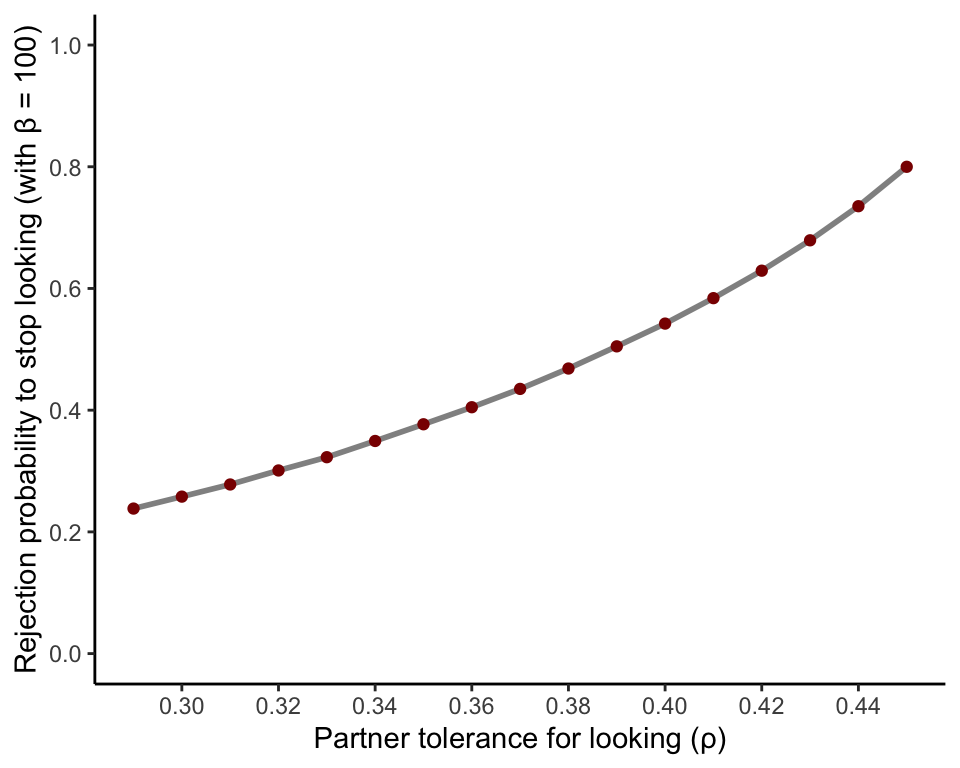
While it’s obvious that having a more lenient partner will extend the range of envelopes that are worth looking into, it’s less obvious why you should be willing to risk a higher probability of rejection when your partner is more lenient. Shouldn’t a high rejection probability deter you from looking, regardless of the specifics of the possible temptations you’re faced with? Surprisingly not. Holding fixed the rejection probability between a lenient and strict partner, the opportunity cost from ignoring the envelope is larger when your partner is more lenient. That is, for any fixed rejection probability, the \(\sigma\) of the temptation distribution will be larger for a more lenient partner, and hence there would be a higher probability of drawing a large reward in the envelope. Therefore, deterrence is less effective, and you should be willing to risk more.
In the real world, it may be difficult to cleanly test this abstract prediction, given the trickiness of measuring the temptation distribution and your partner’s leniency. But to attempt to make this more concrete, let’s return to the example of an acquaintance asking for help moving. Suppose that you’d like to become better friends with this acquaintance so long as the move is going to take less than five hours. Your noisy current estimate is that the move will take only around four hours, so if you couldn’t find out more about the length of the move without ending the friendship, you’d prefer to commit to helping. Still, you are quite uncertain about whether the move will take longer than five hours, and you’d be tempted to gather more information.
Now, as in the simulations above, let’s consider two possible acquaintances: a stricter and a more lenient one. Let’s suppose that even the more lenient acquitance will end the relationship if you directly ask how long the move will take. But it’s possible you can get away with asking less direct questions, which will be less informative.7 If this acquaintance has a reputation for ending friendships over the slightest questioning of loyalty (low \(\rho\)), you might only be able to get away with asking a very subtle question like, “What time would you need to me to arrive in the morning?” Even if the risk from asking this question is fairly low, the expected benefit is also low. (Unless you get a crazy answer like “4am,” you probably won’t shift your beliefs very much.) So you’re probably better off avoiding the question. In contrast, if the acquaintance is more laid-back or less attentive to your motives (high \(\rho\)), you could take a risk of similar magnitude by asking a more informative, but still somewhat indirect, question (e.g., “Do you think I’ll make it back in time for lunch with my colleague?”). The answer to this more informative question has enough of an expected benefit to motivate you to tolerate some risk of the friendship ending.
Effects of your partner’s decision noise
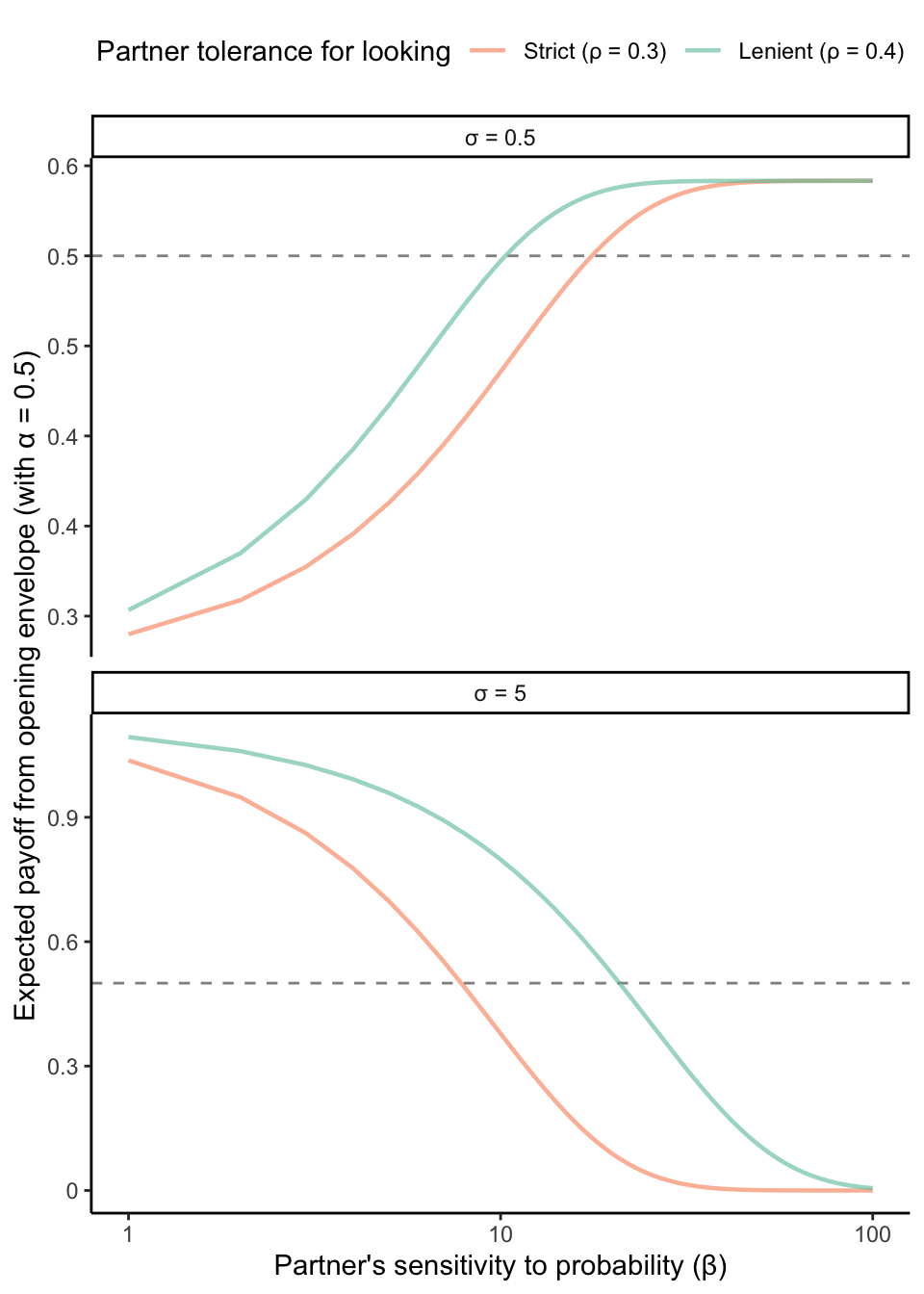
Finally, let’s consider what happens when we lower the sensitivity of your partner to small changes in the envelope distribution — i.e., when we drop \(\beta\) to 10. This turns out to have some striking effects. In fact, the regions where looking dominates not looking almost completely reverse. To see why, first note that, compared to the \(\beta = 100\) case, the risk of rejection begins to increase gradually at lower \(\sigma\) values. Because the opportunity cost of not looking in this parameter region is relatively low, you are deterred from opening the envelope (or at least close to indifferent about opening it). But at higher \(\sigma\) values, the temptation grows at a faster rate than your risk of rejection, which stays well below 100%. This temptation to look overwhelms the deterrent effect from your partner. It’s now worth risking rejection for a higher chance of a large payoff.
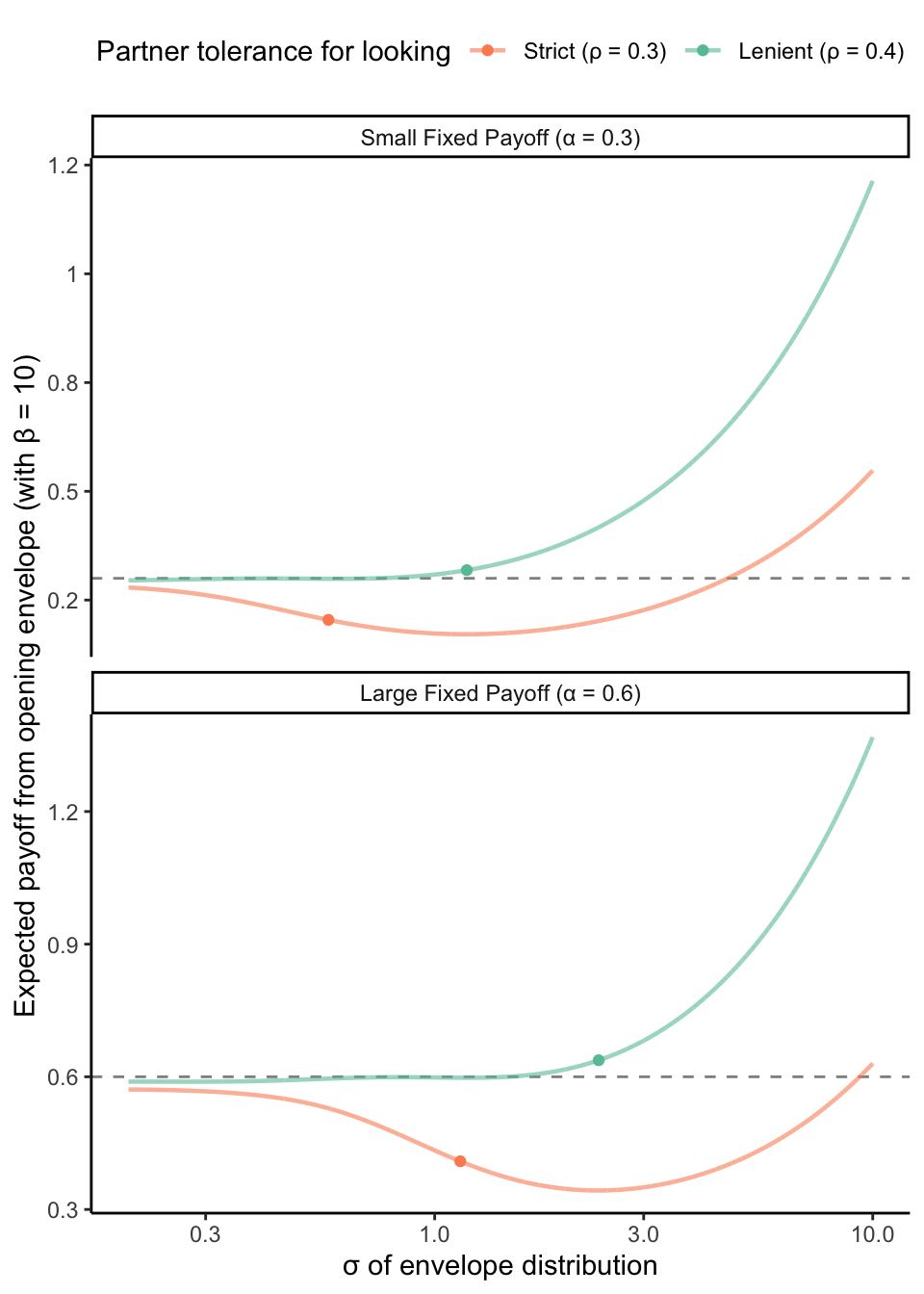
We can see this pattern more clearly below, where we vary sensitivity on the x-axis at a small and a large \(\sigma\) value. Noisy (low \(\beta\)) partners deter looking when temptation is low, and predictable (high \(\beta\)) partners deter looking when temptation is high. If many real-world scenarios resemble the left part of the plot, we may, counterintuitively, expect to see the mostrisky temptation-seeking when partners would most want to deter this kind of behavior.
Conclusion
The logic of Hoffman and colleagues’ envelope game is quite elegant. Even if your partner is better than what you can expect to find by looking elsewhere, it is tempting to explore other options before making a commitment — especially when variability in these outside options is high and, therefore, there’s a reasonable chance of finding someone better from a random draw. But if your partner won’t tolerate your looking at outside options because you might leave them, you would prefer to commit to them, as you prefer them to an expected alternative draw. The variance of alternatives only influences your expected reward if your partner allows you to look, and it is precisely the temptation that comes from this variance that motivates your partner to prohibit you from looking. So, even when variance is high, you stick with your partner simply because they’re better than the average alternative. As the authors nicely state it, “Not looking, in a sense, smooths the temptation to defect; the variability in temptations no longer matters.”
We’ve extended this logic here — modeling the distribution of outside options as continuous (Gaussian) rather than binary and making your partner’s behavior less predictable. In doing so, we uncover a couple of new patterns. First, in modeling your partner’s rejection probability as coming from a logistic function rather than a step function, we find that you should be willing to risk a greater chance of rejection when your partner is willing to risk a higher probability of your leaving them. Second, the predictability of your partner’s behavior (i.e., the steepness of the logistic function) dramatically changes the calculus of when to look. When your partner is less predictable, it turns out that — contradicting the quote above — the variability in temptations matters a lot. You do sometimes want to look even when your partner doesn’t want you to. At the same time, you are sometimes dissuaded from looking even when your partner has a low probability of rejecting you.
There are plenty of further modifications to consider in the future. For example, is it reasonable to assume that the rewards in the envelope are samples from a normal distribution? If you are allowed to peak at multiple possible rewards at any given time step and then pick the best of those, the distribution would be extreme-valued instead of Gaussian, with a longer right tail that could favor more exploration. It could also make sense to explicitly model your partner’s outside options or their bargaining behavior, rather than just assuming they have some exogenous tolerance probability of your leaving them. Lastly, to expand on the results about decision noise, we could add a strategic element to your partner’s enforcement behavior; e.g., perhaps they could intentionally appear noisy to discourage you from exploration when the temptation to explore is already low.
While none of the results here undermine the basic conclusions of the original envelope game, they add nuance that I hope will encourage more targeted predictions about the fascinating logic of strategic ignorance.8
It’s important to note that the ‘temptation’ here is not necessarily a proximate psychological drive you have. It’s an abstract way to describe a class of behaviors that could improve your long-run prospects (in an ultimate evolutionary sense), even if this isn’t something you consciously desire. Indeed, the model is meant to show that there are conditions under which it would be harmful for you to have a proximate drive to seek out other options.↩︎
Note that, while information gathering in the model is likened to ‘looking’ into an envelope, this is a metaphor for any kind of information gathering. While you could be literally looking at other people, you could also be, e.g., asking your colleague whether they’re single.↩︎
This is also quite reminiscent of the economist Robert Frank’s work on the logic of emotions.↩︎
Conceptually, this so-called “partner” could be a friend, colleague, lover, or purely transactional other party who you’re considering making a commitment to. In some contexts, “partner” is not really an accurate description, but I will refer to them as such for brevity.↩︎
In the original game, the fixed reward comes from repeated interaction, so what we’re call \(\alpha\) is actually the product of some smaller payoff \(a\) and some expected number of rounds of a repeated game. But, as far I know, there’s no mathematical reason to explicitly model this product. Also, I’m glossing over some nuance about “cooperation” and “defection” here, which I don’t believe is essential to understand the math.↩︎
My friend Jill helpfully points out that there could be an equilibrium (e.g., from bargaining with a partner) in which your partner is unwilling to tolerate even a small probability that you find useful information by looking into the envelope. In these cases, although your partner is less concerned that you’ll find an exceptional payoff, you are also less tempted to look. So your partner has more leverage to persuade you not to look.
I agree that this plausible bargaining mechanism is lacking in our simple model, and a more complex model should address this issue. At the same time, if we take ‘looking into the envelope’ to be a metaphor for any kind of information gathering, however slight, it seems unlikely that your partner could categorically ban all forms of looking. For example, in a romantic context, you are likely to be able to get away with brief glances at other strangers or indirect questions about which of your acquaintances is single. But this information on its own is unlikely to lead to a better relationship, in contrast to more overt behaviors that your partner could more easily detect and prohibit, such as going on a dating app or going to a bar alone.↩︎To avoid taking us too far afield, I’m not delving deep into the connections between this example and the math of the envelope game. But, in short, I’m assuming that asking a less informative question is akin to opening a less tempting envelope (an envelope with lower \(\sigma\)). To understand how this works, we need to characterize your belief about the move length as a probability distribution over move times (centered on four hours, but with wide confidence intervals that include times well above five hours). We further need to assume that your acquaintance has a decent estimate of this distribution, as they are modeling the temptation from your vantage point. They, of course, have a much better sense of whether the move will take longer than five hours, but this isn’t relevant to their appraisal of you. They could be upset with you even if they know the move will only take around two hours, but they believe that you believe it could take much longer than this and are trying to find out the answer.
In this framework, the temptation from asking a question is your estimated likelihood that the answer to your question would move the mean of your belief distribution to a time greater than five hours, which is the threshold at which you’d prefer to bail on the relationship. If you could ask about the move time directly, you might estimate that the answer to this question would have around a 45% probability of shifting your expected belief above five hours — too high a temptation for even the more lenient partner in our example to tolerate. In contrast, indirect questions are less likely to move your expected belief far from your current expectation of four hours, and they are therefore less tempting and less threatening to the acquaintance.↩︎
