In my last post, I discuss the motivation for using cumulative ordinal regression models to represent ordinal dependent measures, such as Likert responses. I argue that we should prefer these models to more common models, such as OLS, because they appropriately treat the ordinal values as an incomplete proxy for the latent continuous construct that we want to measure.
But we might guess that there’s minimal harm in pretending that this ordinal proxy is identical to the latent construct. For example, if we wanted to compare Likert ratings from two conditions of an experiment, the difference in the means of the Likert ratings should be pretty similar to the difference in the latent means of the two groups. Or, at the very least, this difference should have the same sign as the difference between the latent means, so we won’t get fooled into thinking an effect is in one direction when it’s actually in the other direction. Right?
Wrong. While doing my research on ordinal models, I stumbled upon this paper, which reports a surprising fact: when a measure is ordinal, a difference between group means on the ordinal scale can be completely explained by a difference in variances of the latent distributions that underlie these group responses. And, in fact, when the latent variances are different, the difference of the ordinal means can have the opposite sign of the difference of the latent means.
Practically speaking, this means that if we’re naively comparing the averages of two groups’ responses measured with Likert scales, any putative difference could be illusory or even in the wrong direction from the latent construct we’re trying to measure. For example, it could seem as if there’s a gender difference in a trait or attitude when it’s actually just the case that, say, men give more variable responses than women. Or an intervention that ostensibly increases one’s intention to engage in a healthy behavior could actually just be producing more polarization in intentions. And so on.
To make matters worse, a simple ordinal regression model won’t solve this problem. Without the addition of further bells and whistles that will be anathema to most social scientists, such models will assume a constant latent variance and therefore suffer from the same issue as OLS.1 What can we do instead? In this post, I will describe a quick (but imperfect) trick to diagnose the issue, but ultimately, only a rather sophisticated model can fully address the problem.
The intuition
How can a difference in latent variances cause a spurious difference in ordinal means? Before diving in to the specific issue with ordinal values, let’s consider a simpler case involving censored variables. Suppose we have responses sampled from a continuous, normally distributed distribution that is left- and right-censored at -1 and +1, respectively. This means that any latent value that is less than -1 will show up as -1 in our data set, and any latent value greater than +1 will show up as +1 in our data set. We want to estimate the mean of the latent variable, not the censored variable.
The extent to which the mean of the censored variable deviates from the mean of the latent variable will depend on the variance of the latent distribution, along with the mean. To see this, imagine that the latent mean is 0.2. If the variance of the distribution is very low such that most points hover near this mean (solid line below), censored values will be rare, and the censored mean will be a decent approximation of the latent mean. In contrast, if the variance of the distribution is large (dotted line), we are likely to find many +1s and -1s in our data, which will complicate estimation of the latent mean. In particular, since the mean is positive, there will be more censored +1s than -1s, and these +1s will bias the estimate downwards.
ggplot() +
geom_vline(xintercept = c(-1, 1), color = "darkred", alpha = 0.5) +
stat_function(
fun = \(x) dnorm(x, 0.2, .3),
xlim = c(-4, 4),
) +
stat_function(
fun = \(x) dnorm(x, 0.2, 1.3),
xlim = c(-4, 4),
linetype = "dashed"
) +
labs(y = element_blank()) +
scale_x_continuous(breaks = -3:3) +
scale_y_continuous(breaks = NULL) 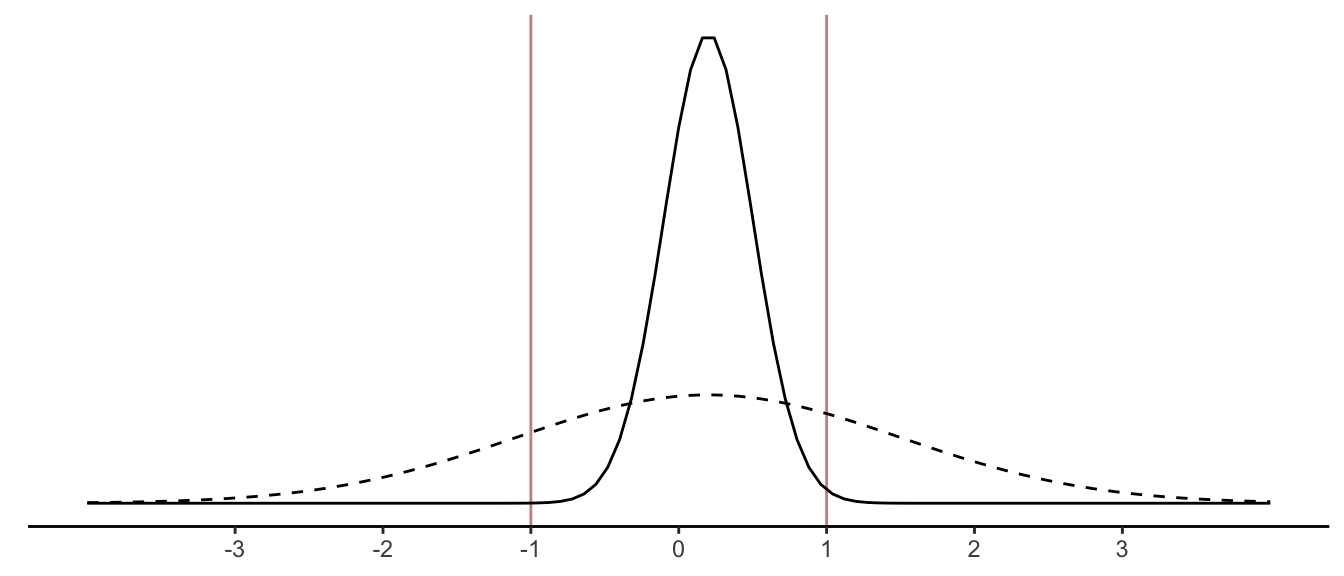
We can see this effect more clearly if we jointly change the mean and variance. In the plot below, the censored means converge towards zero as the square rooted variance (standard deviation) increases. But even before the variance gets particularly large, the censored mean is shrunk in absolute terms relative to the latent mean, which can create situations where a group with a higher latent mean with large latent variance has a lower censored mean than a group with a lower latent mean with small latent variance. For example, when the latent standard deviation is 1, the top line, which corresponds to a latent mean of 0.5, has a censored mean that falls below the censored mean of the latent mean of 0.4 line with standard deviation of 0.1.
censored_mean <- function(latent_mean, latent_sd,
left_censor = -1, right_censor = 1) {
xs <- seq(-100, 100, .01)
normal_probs <- dnorm(xs, mean = latent_mean, sd = latent_sd)
normal_probs <- normal_probs / sum(normal_probs) # normalize to be PMF
intermediate_probs <- normal_probs[xs >= left_censor & xs <= right_censor]
# return censored expected value
left_censor * pnorm(left_censor, mean = latent_mean, sd = latent_sd) +
right_censor * (1 - pnorm(right_censor, mean = latent_mean, sd = latent_sd)) +
sum(xs[xs >= left_censor & xs <= right_censor] * intermediate_probs)
}
df_params <- crossing(
latent_mean = seq(-0.5, 0.5, 0.1),
latent_sd = seq(0.05, 10, 0.05)
) |>
mutate(
censored_mean = map2_dbl(latent_mean, latent_sd, censored_mean)
)
ggplot(df_params, aes(latent_sd, censored_mean, color = latent_mean)) +
geom_line(aes(group = latent_mean)) +
labs(
x = "Latent Standard Deviation",
y = "Censored Mean",
color = "Latent Mean"
) +
scale_x_log10() + # plot x on log scale
scale_y_continuous(breaks = seq(-1, 1, 0.1)) +
theme(legend.position = "bottom")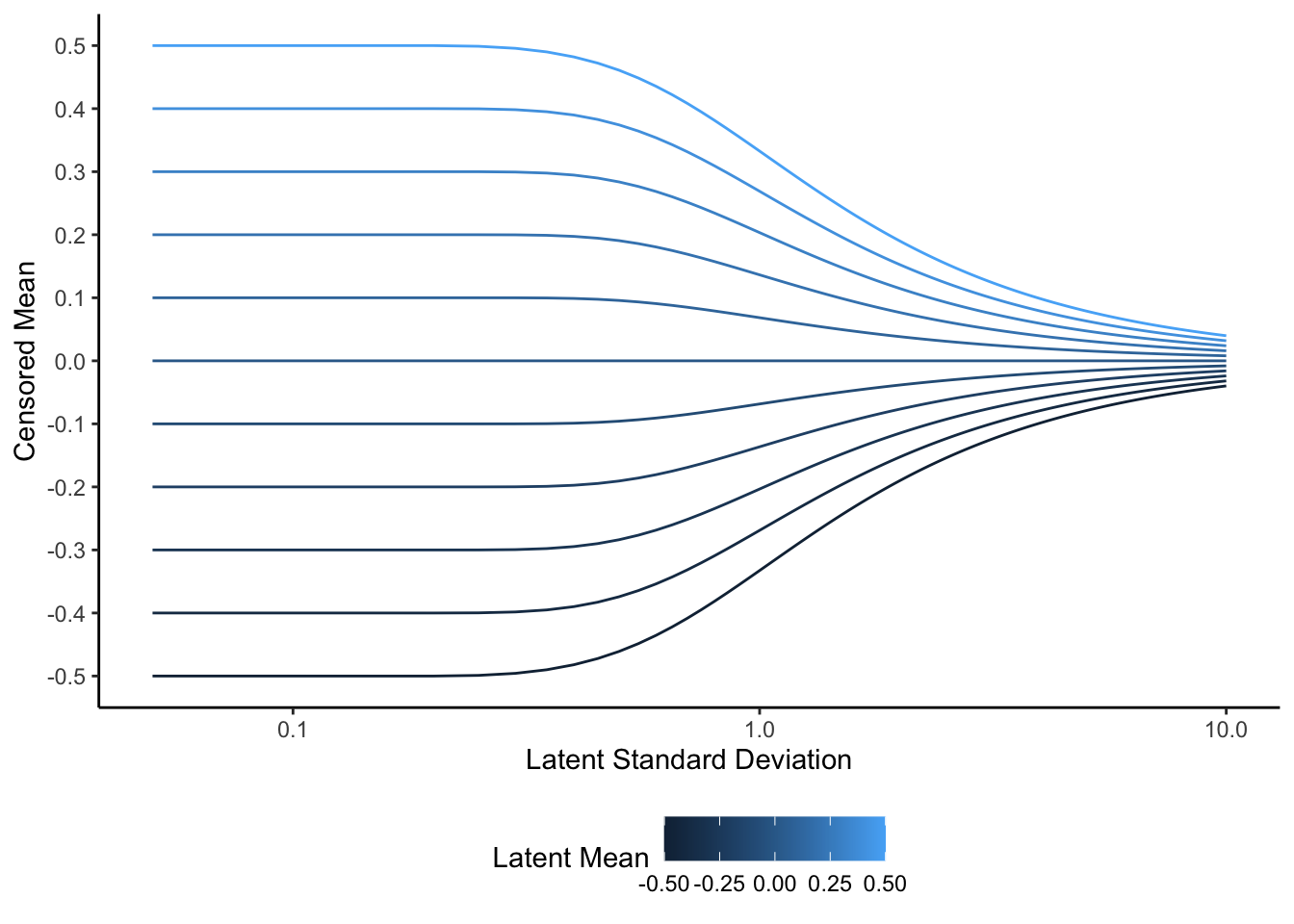
Ordinal variables suffer from essentially the same issue as censored variables, with further complications. The lowest and highest values behave like left- and right-censored values, and the interior values are interval censored; i.e., they only indicate that a latent value is within some range. But the issues we’ll focus on here are primarily about the left- and right-censoring.
Ordinal regression to the rescue?
In a previous post, I explained how the brms package can be used to run a Bayesian (cumulative) ordinal probit model to estimate latent means and differences. But I mentioned that the default model this package fits fixes the variance of all groups at 1 and models how cutpoints all shift a fixed distance left or right. This is a necessary assumption if we want the model to estimate all k - 1 cutpoints, as a change in the latent variance cannot be distinguished from a change in the scale of the cutpoints. That is, the variance is not identifiable by the model if all cutpoints are also estimated.
How harmful is this assumption of uniform variances? Let’s simulate a scenario where the latent variances differ between groups. I’ll assume one of the latent means is 4.2 with a standard deviation of 3, and the other latent mean is 3.9 with a standard deviation of 0.5. Samples from these latent distributions are mapped to a 5-point Likert scale, with somewhat arbitrarily chosen cutpoints at 1.3, 3.1, 3.5, and 4.2. That is, latent values less than 1.3 get mapped to 1; those between 1.3 and 3.1 get mapped to 2; and so on. (If you’re worried about the arbitrariness of my choices here, we’ll do a more systematic exploration later.)
set.seed(42)
n <- 1000
mu0 <- 4.2; sd0 <- 3
mu1 <- 3.9; sd1 <- 0.5
df_dif <- tibble(
dummy = rep(c(0, 1), each = n / 2), # binary predictor
z = c(rnorm(n / 2, mean = mu0, sd = sd0), # latent var
rnorm(n / 2, mean = mu1, sd = sd1)),
y = findInterval(z, c(-Inf, 1.3, 3.1, 3.5, 4.2, Inf)) # Likert var
)First, we can observe that the means of the ordinal variables are opposite those of the latent variables; hence, a standard OLS will yield the incorrect sign.
df_dif |>
summarize(mean_y = round(mean(y), 1), .by = dummy) |>
mutate(true_means = c(mu0, mu1))## # A tibble: 2 × 3
## dummy mean_y true_means
## <dbl> <dbl> <dbl>
## 1 0 3.5 4.2
## 2 1 4 3.9If we run a standard ordinal model, we get the following results:
brm(
y ~ dummy, data = df_dif,
family = cumulative("probit"),
cores = 4, chains = 4, iter = 2000,
file = "Models/likert_probit_novar"
) |>
fixef(pars = "dummy")## Estimate Est.Error Q2.5 Q97.5
## dummy 0.2022883 0.07051696 0.06899128 0.3402969Alas — just like OLS, the ordinal model spuriously identifies a positive effect of the dummy, which is actually a consequence of a difference in latent variances.
This problem can be solved by telling brms to also allow the variance to depend on the dummy2:
brm(
bf(y ~ dummy) + lf(disc ~ dummy), data = df_dif,
family = cumulative("probit"),
cores = 4, chains = 4, iter = 2000,
file = "Models/likert_probit_withvar"
) |>
fixef(pars = "dummy")## Estimate Est.Error Q2.5 Q97.5
## dummy -0.2802171 0.451021 -1.334759 0.5296519This model does a good job recovering the true difference between latent means, albeit with a lot of posterior uncertainty. Unfortunately, I suspect that a lot of researchers will not be too keen to write some bespoke brms code whenever they want to compare two Likert groups. Is there any workaround?
A shortcut
For researchers who don’t want to deal with the intricacies of Bayesian modeling, I suggest doing a quick test for each Likert group whose mean needs to be estimated. Although this test is rooted in the same logic as the cumulative ordinal model, it doesn’t require building a custom model; all it requires is the counts of each Likert category.
Here’s how the test works. Recall that, for a single group, the cutpoints of a cumulative ordinal probit model are values in an unbounded latent “probit” space. Practically speaking, this means that the values of the cutpoints can be mapped in a one-to-one fashion to cumulative probabilities of the standard normal distribution (i.e., a normal distribution with a mean of zero and unit variance). This is convenient, as we can directly estimate cumulative probabilities from our data. First, we can use the table function to get counts of all Likert categories. Then, we transform these counts into cumulative sums, which we divide by the total number of responses to get cumulative probabilities. We can pass these cumulative probabilities into the quantile function for the standard normal distribution, qnorm, to turn them into estimated probit thresholds.
If you try this procedure on a single group in your data — provided you have a sufficient spread of counts across all Likert categories — you should find that the thresholds you get out are basically the same as what you get from running an intercept-only model (e.g., in brms). But these are thresholds for a distribution with zero mean and unit variance. If we want to allow the mean and variance to themselves be estimated, we need to fix two of our thresholds at pre-specified values because of the identifiability issues mentioned earlier. Liddell and Kruschke choose to fix the leftmost and rightmost thresholds at the midpoints between the two leftmost and two rightmost scale points, respectively. For a 1 to 5 Likert scale, this would correspond to 1.5 and 4.5. In other words, instead of estimating the two most extreme thresholds, we can assume that latent values less than 1.5 get mapped to a Likert rating of “1” and latent values greater than 4.5 get mapped to “5.”
It’s straightforward to transform our estimated probit thresholds into a new latent space that has these extreme thresholds fixed. We need to stretch or squeeze the thresholds to the width of our fixed thresholds (4.5 - 1.5 = 3 in our example), and then shift the thresholds left or right so that the leftmost threshold matches the fixed value (1.5 in our example).
Concretely, imagine our leftmost probit threshold is -2 and rightmost threshold is 2.5. We first need to squeeze the distance between these thresholds (4.5) to be equal to the distance between our new fixed thresholds (3). We then need to shift these rescaled thresholds to the right such that the smallest threshold equals 1.5. The factor we need to scale the probit thresholds (3/4.5 = 2/3) is our estimated latent standard deviation, and the factor we need to shift them (1.5 - (-2) * (2/3) = 17/6) is our estimated latent mean.
If this is confusing, rest assured that we can bundle all these steps into a simple function that takes in Likert category counts3 and outputs an estimated mean and standard deviation:
get_latent_parameters <- function(dv_counts, left_threshold, right_threshold) {
thresholds <- qnorm( # convert cumulative probs to probit scale
cumsum(dv_counts / sum(dv_counts))[-length(dv_counts)]
)
scale_factor <- (right_threshold - left_threshold) /
(thresholds[length(thresholds)] - thresholds[1])
shift_factor <- left_threshold - thresholds[1] * scale_factor
tibble(inferred_mean = shift_factor, inferred_sd = scale_factor)
}We can give this function a whirl with our two dummy groups from above. Let’s imagine that we don’t know the actual cutpoints and, hence, we default to setting the left and right thresholds at 1.5 and 4.5.
df_dif |>
filter(dummy == 0) |>
pull(y) |>
table() |>
get_latent_parameters(left_threshold = 1.5, right_threshold = 4.5)## # A tibble: 1 × 2
## inferred_mean inferred_sd
## <dbl> <dbl>
## 1 4.28 2.94df_dif |>
filter(dummy == 1) |>
pull(y) |>
table() |>
get_latent_parameters(left_threshold = 1.5, right_threshold = 4.5)## # A tibble: 1 × 2
## inferred_mean inferred_sd
## <dbl> <dbl>
## 1 3.68 1.44As we can see, this heuristic method performs decently. It identifies that the variance of the first group is much larger than that of the second group. And more importantly, it identifies that the mean of the first group is larger than that of the second group. These estimates aren’t perfect, but if we ran this analysis as a check on a simple OLS model, it might make us think twice about the positive dummy estimate that our model returned.
Evaluating performance
Let’s do a more systematic — albeit still limited — test of this heuristic method. The aim here is not to explore a huge space of different latent means and variances, but to home in on the problematic parameter region where (a) the difference in means between groups is fairly small (as is often in the case in the social sciences) and (b) the difference in variances is large. I exaggerate the difference in variances to a perhaps unrealistic degree to highlight how our heuristic method differs from a naive difference in ordinal means, but I would expect problems to emerge even when the difference in variances is smaller.
Below, I write a function to simulate ordinal data with a latent mean, latent standard deviation, and randomly chosen cutpoints. I consider simulated groups in which the latent mean of one group is sampled from a normal distribution with a mean of 3.8, and the mean of the other group is sampled from a normal distribution with a mean of 4.2, resulting in an expected mean difference between groups of 0.4, with considerable variation across groups. I sample the standard deviations from exponential distributions with the rate parameter varying by a factor of 4.
For each simulated group, we can compare the true latent mean difference that we want to estimate to the (a) difference in ordinal means (i.e., what you’d get out of OLS or a t-test) and (b) difference in inferred latent means via our heuristic method.4
# Function to simulate ordinal data
simulate_ordinal_data <- function(n, latent_mean, latent_sd,
n_scale_pts = 5, cutpoints = NULL) {
# if cutpoints aren't provided, create uniformly random ones
cutpoints <- cutpoints %||% sort(runif(n_scale_pts - 1, 1, n_scale_pts))
# surround internal cutpoints with -Inf and Inf for `findInterval`
cutpoints <- c(-Inf, cutpoints, Inf)
# latent variable
z <- rnorm(n, mean = latent_mean, sd = latent_sd)
# return ordinal data
findInterval(z, cutpoints)
}
# Run 10k simulations
set.seed(3233)
n_sims <- 10000 # number of simulations
n_pts <- 1000 # data points per simulations
n_scale_pts <- 5
df_latent_ests <- tibble(
group = rep(seq_len(n_sims / 2), each = 2),
latent_mean = rnorm(n_sims, rep(c(2.8, 3.2), n_sims / 2), 0.2),
latent_sd = rexp(n_sims, rep(1 / c(1, 4), n_sims / 2)),
cutpoints = rep(map(
seq_len(n_sims / 2),
~ sort(runif(n_scale_pts - 1, 1, n_scale_pts))
), each = 2)
) |>
rowwise() |>
mutate(
simulated_data = list(
simulate_ordinal_data(n_pts, latent_mean, latent_sd, cutpoints)
),
simulated_mean = mean(simulated_data),
inferred_params = list(
simulated_data |>
table() |>
get_latent_parameters(1.5, 4.5)
)
) |>
unnest_wider(inferred_params) |>
summarize(
true_mean_dif = latent_mean[2] - latent_mean[1],
simulated_mean_dif = simulated_mean[2] - simulated_mean[1],
inferred_mean_dif = inferred_mean[2] - inferred_mean[1],
.by = group
) |>
mutate(
mean_error = inferred_mean_dif - true_mean_dif,
correct_inferred_sign = sign(true_mean_dif) == sign(inferred_mean_dif),
correct_mean_sign = sign(true_mean_dif) == sign(simulated_mean_dif)
)Let’s see how well our two estimation methods reproduce the true latent mean difference. We can do this by first looking at the raw estimate (top plot) and then by looking at the probability of getting the sign correct (bottom plot).
# plot of true mean dif predicting inferred mean dif & simulated mean dif
p1 <- df_latent_ests |>
select(ends_with("mean_dif")) |>
filter(!is.na(inferred_mean_dif), !is.infinite(inferred_mean_dif)) |>
pivot_longer(!true_mean_dif, names_to = "metric", values_to = "mean_dif") |>
ggplot(aes(x = true_mean_dif, y = mean_dif, color = metric)) +
geom_abline(linetype = "dashed", alpha = 0.5) +
geom_point(size = 0.3, alpha = 0.2) +
coord_cartesian(xlim = c(-1, 1.5), ylim = c(-5, 5)) +
labs(
x = "True difference in latent means",
y = "Difference in inferred means",
color = "Method"
) +
scale_color_brewer(
palette = "Set2",
labels = c("Latent Estimates", "Likert Means")
) +
guides(color = guide_legend(override.aes = list(size = 3, alpha = 1))) +
theme(legend.position = "bottom")
# plot of sign errors for each strategy
p2 <- df_latent_ests |>
filter(!is.na(inferred_mean_dif), !is.infinite(inferred_mean_dif)) |>
mutate(abs_true_dif = abs(true_mean_dif)) |>
select(abs_true_dif, ends_with("sign")) |>
pivot_longer(
!abs_true_dif,
names_to = "metric", names_prefix = "correct_",
values_to = "correct",
values_transform = list(correct = as.numeric)
) |>
ggplot(aes(x = abs_true_dif, y = correct, color = metric)) +
geom_hline(yintercept = 0.5, linetype = "dashed", alpha = 0.5) +
geom_point(size = 0.1, alpha = 0.2) +
geom_smooth(
method = "glm", method.args = list(family = "binomial")
) +
labs(
x = "True absolute difference in latent means",
y = "Probability of correctly inferred direction",
color = "Method"
) +
scale_color_brewer(
palette = "Set2",
labels = c("Latent Estimates", "Likert Means")
) +
theme(legend.position = "bottom")
p1 / p2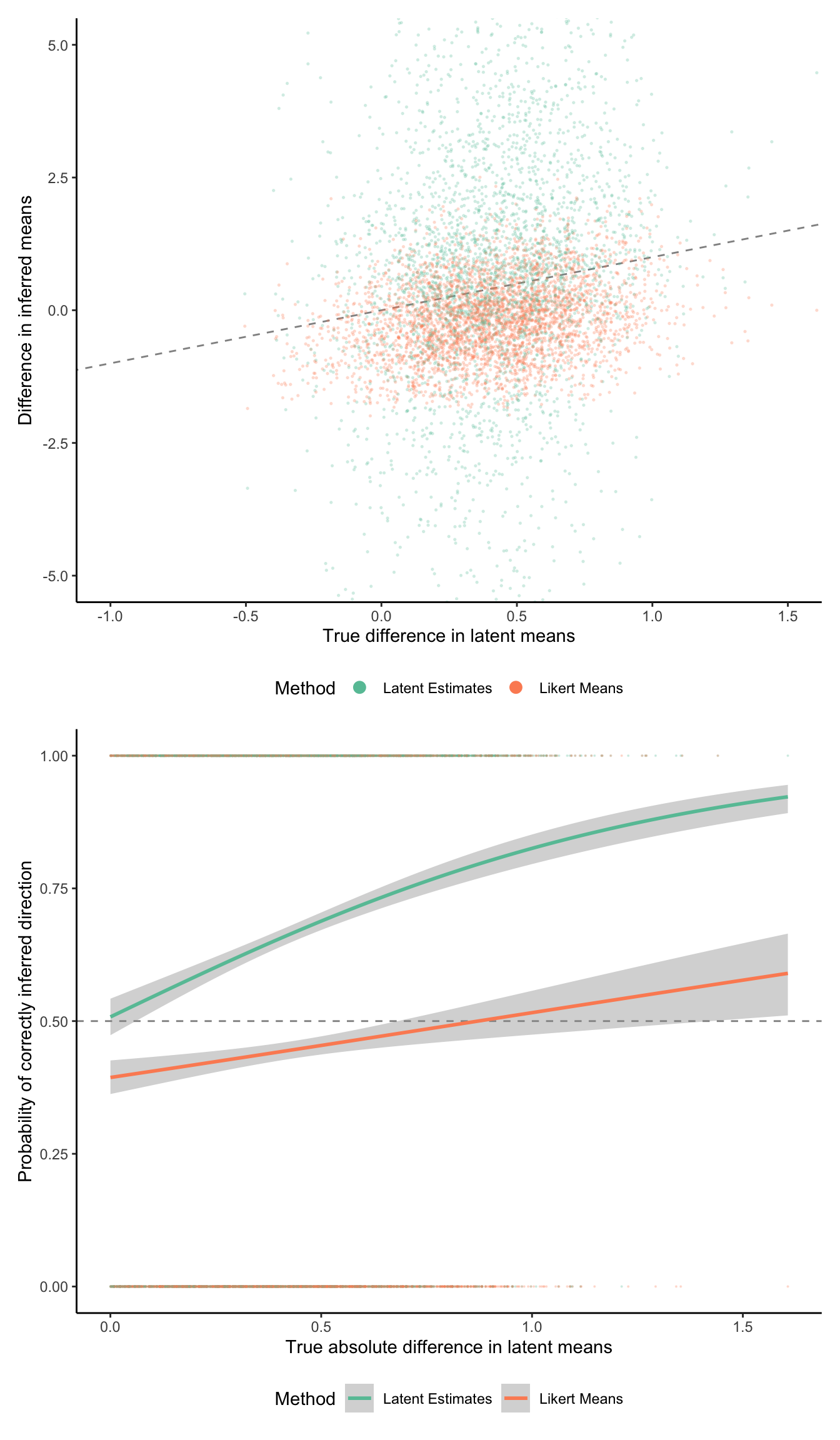
In this simulated region of parameter space, it’s clear that the heuristic of inferring latent means outperforms the naive method of simply averaging the ordinal values. Indeed, when the latent difference in means is small, the naive method is below chance at estimating the direction of the effect. However, the heuristic method does seem to suffer from more unsystematic error, with points scattered far and wide. As I note in the footnote above, I suspect that some of this noise could be smoothed out by adding pseudo-counts to the empirical counts of each Likert category, but this is a topic for another day.
Conclusion
Liddell and Kruschke ask “what could possibly go wrong” when psychologists model ordinal (e.g., Likert) data with commonly used metric models (t-tests, OLS, etc.). Although the question suggests a general problem, it turns out that the wrongness of metric models is the most pronounced when the groups being compared have different latent variances. Unfortunately, just plugging ordinal data into an off-the-shelf ordinal regression function that we might find in an R package (even a Bayesian one, such as brms) won’t actually address this issue, as such models will assume a fixed variance across groups. Liddell and Krusche are quite explicit that the variance of each group needs to be estimated, and they even provide thorough code that does this modeling. Yet I worry that the general point may be lost for more causal readers, and the custom code may deter researchers from investing in this kind of modeling.
If researchers don’t want to delve deep into complex ordinal modeling, they are left with few options. One option is to simply ignore the problem and hope that the latent variances between groups are not substantially different. This is the approach that almost all psychologists take, and for all I know, it may be fine. To my knowledge, nobody has systematically explored the latent variances of groups in psychological studies, and perhaps these variances don’t differ enough to matter in the contexts that researchers care about.5
Nevertheless, it may be worth at least trying the heuristic method I describe above. While this method is flawed and shouldn’t be taken as a reliable estimate, it could act as a warning sign that an observed difference in means is spurious.
Recall that in the standard models discussed in my last post, the variance is not identifiable when the model is also fitting all k - 1 cutpoints. However, as I discuss below, we can fix two of the cutpoints to fit a mean and variance if desired.↩︎
Or, technically, have the dummy predict the log of the
discparameter, which is the reciprocal of the square root of the variance.↩︎When using this function, make sure that there are nonzero counts for all possible Likert categories. And because the cumulative probabilities are estimated from data, our estimated means and variances will be more error prone if some Likert values have very few responses.↩︎
The heuristic method sometimes failed by returning an NA or infinite value, in which case I dropped the simulated run. In the future, I might consider how we could reduce such occurrences by adding pseudo-counts to the ordinal counts, which is effectively like incorporating a prior into the estimates that smooths out noise.↩︎
Liddell and Krusche did find an alarming amount of heterogeneity in the variances of latent Amazon ratings, however.↩︎